Distributed Key Generation

A prerequisite for flow encryption in Penumbra is some distributed key generation algorithm. Our threshold encryption scheme uses ElGamal and operates over the decaf377 group, thus we must choose a DKG which operates over decaf377 outputs a decaf377 public key.

Desired Properties

Minimal Round Complexity

The DKG must be run by all validators at the start of every epoch. Ideally, the DKG should be able to run in over a single block, such that there is no delay between the start of the epoch and when users can delegate in the staking system or trade on ZSwap. As such, for optimal UX and simplicity of implementation, the optimal DKG for our scheme should have minimal round complexity. Each round of communication can occur in the ABCI++ vote extension phase. Since Tendermint votes already impose an O(n^2) communication complexity for each block, minimal communication complexity is not important for our DKG.

Verifiability and Security Under Rogue-Key Attacks

In addition to minimal round complexity, our DKG must be verifiable: participants (validators) must be able to verify that counterparty participants (other validators) are contributing to the DKG honestly, without the use of a trusted dealer. This can be achieved using something similar to Feldman’s Verifiable Secret Sharing protocol, where each participant shares a commitment to their share which is visible to all other participants. In addition, our DKG must be able to tolerate rogue-key attacks: that is, it must tolerate the instance where a validator maliciously chooses their share based on the value of the other validator’s shares in order to cancel out other validator’s keyshares and gain unilateral control over the resulting DKG key. One way this can be prevented is by each validator producing a proof of knowledge of their secret share.

Robustness

An additional property that our DKG should have is that of robustness. The DKG should be able to tolerate a byzantine threshold of validators intentionally refusing to participate in the DKG round, or intentionally contributing malformed shares during DKG execution, without requiring a full restart of the DKG protocol. This is due to DoS concerns: with a naive, non-robust implementation, a single malicious validator could potentially indefinitely delay the beginning of an epoch by refusing to participate in DKG or by contributing invalid shares.

A Survey of Existing DKGs

Gurkan, Jovanovic, Maller, Meiklejohn, Stern, and Tomescu present a survey of DKG instantiations with their communication complexity, public verifiablity, round complexity, prover, and verifier costs:

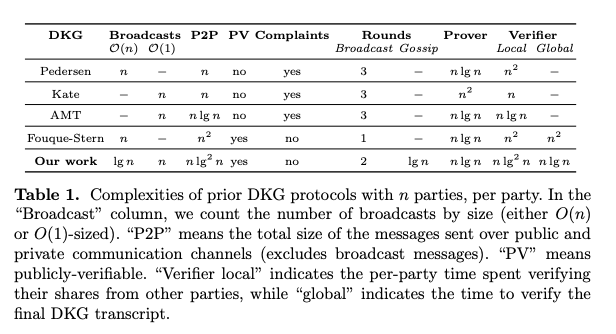
Note that PV, public verifiability, is slightly different than our requirement of verifiability: public verifiability means that any non-participating observer must be able to verify the correct execution of the DKG.

Of the schemes listed, Fouque-Stern has the lowest round complexity, however the scheme uses Pallier which is not compatible with our encryption scheme. The scheme described in that paper uses pairings, and thus is also not compatible with our scheme. In addition, O(n*log*n) communication complexity is not important for our scheme, since our vote extensions already require n^2 communication.

In addition to these schemes, ETHDKG is in use by Anoma and Osmosis in Ferveo. However, this scheme is also not applicable to our threshold encryption scheme as it is based on pairings rather than a discrete log DKG.

FROST

Komlo and Goldberg introduced FROST: Flexible Round-Optimized Schnorr Threshold Signatures. FROST contains a DKG which is a slightly modified version of Pedersen’s DKG, modified to protect against rogue-key attacks. FROST DKG operates on any prime order group where Decisional Diffie-Hellman is difficult, and thus is compatible with decaf377.

Verifiability

FROST DKG fulfills the requirement of verifiability and security under rogue-key attacks. FROST DKG achieves this by slightly modifying Pedersen’s DKG to include a proof of knowledge of each participant’s secret in the first round of communication.

Robustness

FROST DKG trades off simplicity and efficiency in favor of robustness. A single participant can cause the DKG to abort by contributing an invalid share or by refusing to produce a key share. Gennaro, Jarecki, Krawczyk, and Tal Rabin presented an alternative instantiation of Pedersen’s DKG, which can tolerate up to n-t invalid or missing shares. This is accomplished by adding an additional complaint round, where participants can publish evidence of a participant’s invalid contribution and disqualify them from the DKG. A similar strategy could be added to FROST DKG to adapt it to be robust.

Round Complexity

By including an additional round for relaying complaints from each participant to each counterparty, the round complexity of our DKG rises to 3 rounds.

ABCI++ Implementation

A prerequisite for implementing any DKG scheme in Penumbra is ABCI++, the extension to Tendermint which adds additional hooks to the Tendermint state machine interface, most importantly vote extensions.

Implementing FROST DKG with ABCI++ can be done naively by placing each round of communication in the Vote Extensions phase of ABCI++. This gives an upper bound on the delay between the start of a new epoch and the completion of the DKG as 3 blocks: 1 block per vote extension communication round.

This could potentially be pipelined by including each participant’s commitments for the next epoch (the commitments $a_{ij}\ast G$ from FROST) in the block data at one of the last blocks of the previous epoch. Round 2 of FROST could occur during the vote extensions phase of the epoch transition block.

NOTE: FROST requires private communication channels for round 2, thus we must assign validators encryption keys, perform key agreement, and encrypt round 2 communications before placing them in the vote extension. This can be accomplished using ECDH with decaf377, and an AEAD cipher (though authentication is not strictly required, since vote extensions are signed).

TODO:

[] concrete robust FROST implementation