Poseidon Parameter Generation

The problem of Poseidon parameter generation is to pick secure choices for the parameters used in the permutation given the field, desired security level $M$ in bits, as well as the width $t$ of the hash function one wants to instantiate (i.e. 1:1 hash, 2:1 hash, etc.).

Poseidon parameters consist of:

• Choice of S-box: choosing the exponent $\alpha$ for the S-box layer where $S(x)=x^{\alpha }$,
• Round numbers: the numbers of partial and full rounds,
• Round constants: the constants to be added in the AddRoundConstants step,
• MDS Matrix: generating a Maximum Distance Separable (MDS) matrix to use in the linear layer, where we multiply this matrix by the internal state.

Appendix B of the Poseidon paper provides sample implementations of both the Poseidon permutation as well as parameter generation. There is a Python script called calc_round_numbers.py which provides the round numbers given the security level $M$, the width of the hash function $t$, as well as the choice of $\alpha$ used in the S-box step. There is also a Sage script, which generates the round numbers, constants, and MDS matrix, given the security level $M$, the width of the hash function $t$, as well as the choice of $\alpha$ used in the S-box step.

Since the publication of the Poseidon paper, others have edited these scripts, resulting in a number of implementations being in use derived from these initial scripts. We elected to implement Poseidon parameter generation in Rust from the paper, checking each step, and additionally automating the S-box parameter selection step such that one can provide only the modulus of a prime field and the best $\alpha$ will be selected.

Below we describe where we deviate from the parameter selection procedure described in the text of the Poseidon paper.

Choice of S-Box

The Poseidon paper focuses on the cases where $\alpha =[-1,3,5]$, as well as BLS12-381 and BN254. For a choice of positive $\alpha$, it must satisfy $gcd(\alpha ,p-1)=1$, where $p$ is the prime modulus.

For our use of Poseidon on BLS12-377, we wanted to generate a procedure for selecting the optimal $\alpha$ for a general curve, which we describe below.

We prefer small, positive $\alpha$ for software (non-circuit) performance, only using $\alpha =-1$ when we are unable to find an appropriate positive $\alpha$. For positive $\alpha$, the number of constraints in an arithmetic circuit per S-Box is equal to its depth in a tree of shortest addition chains. For a given number of constraints (i.e. at a given depth in the tree), we pick the largest $\alpha$ at that level that meets the GCD requirement. Since larger $\alpha$ provides more security, choosing the largest at a given depth reduces the round requirement.

The procedure in detail:

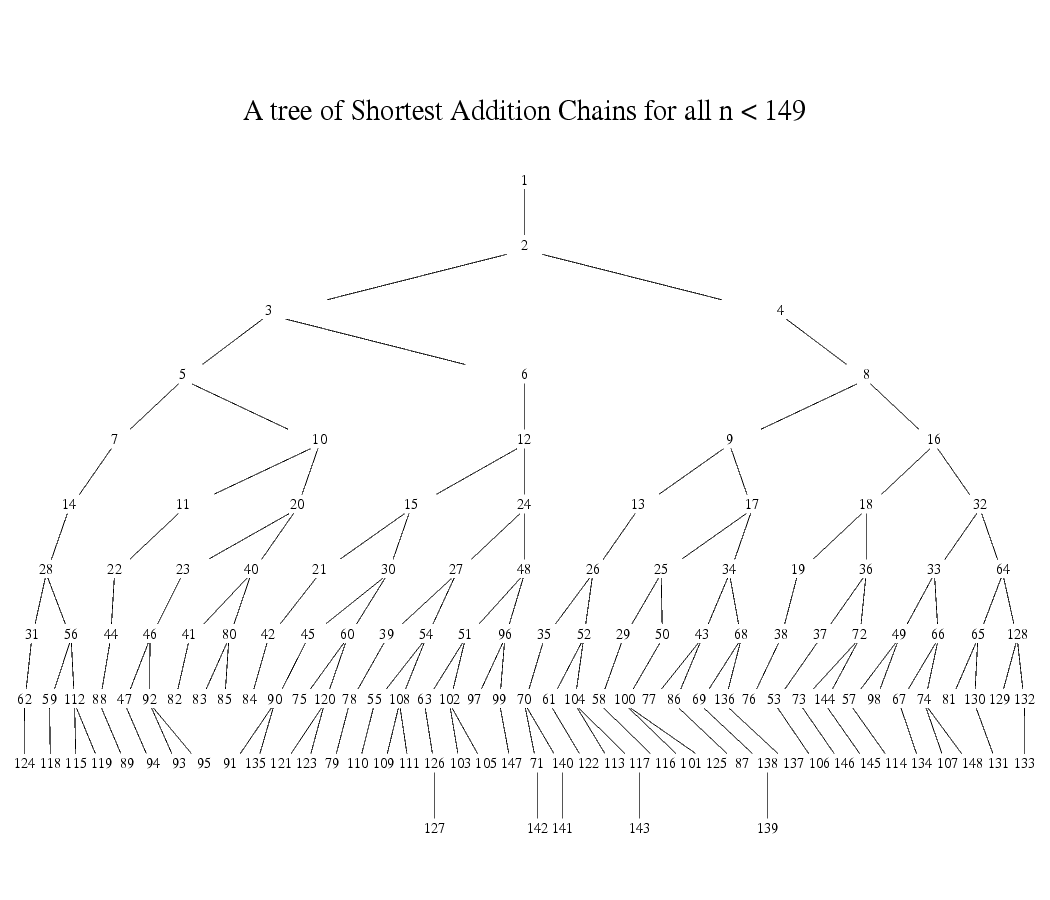
We proceed down the tree from depth 2 to depth 5 (where depth 0 is the root of 1):

1. At a given depth, proceed from largest number to smaller numbers.
2. For a given element, check if $gcd(\alpha ,p-1)=1$ is satisfied. If yes, we choose it, else continue.

If we get through these checks to depth of 5 without finding a positive exponent for $\alpha$, then we pick $\alpha =-1$, which is well-studied in the original Poseidon paper.

For decaf377, following this procedure we end up with $\alpha =17$.

Round Numbers

We implement the round numbers as described in the original paper. These are the number of rounds necessary to resist known attacks in the literature, plus a security margin of +2 full rounds, and +7.5% partial rounds.

We test our round number calculations with tests from Appendices G and H from the paper which contain concrete instantiations of Poseidon for $\alpha =[-1,3,5]$ and their round numbers.

Round Constants

We do not use the Grain LFSR for generating pseudorandom numbers as described in Appendix F of the original paper. Instead, we use a Merlin transcript to enable parameter generation to be fully deterministic and easily reproducible.

We first append the message "poseidon-paramgen" to the transcript using label dom-sep.

We then bind this transcript to the input parameter choices:

• the width of the hash function $t$ using label t,
• the security level $M$ using label M, and
• the modulus of the prime field $p$ using label p.

We then also bind the transcript to the specific instance, as done with the Grain LFSR in Appendix F, so we bind to:

• the number of full rounds $R_F$ using label r_F,
• the number of partial rounds $R_P$ using label r_P, and
• the choice of S-box exponent $\alpha$ using label alpha.

We generate random field elements from hashes of this complete transcript of all the input parameters and the derived parameters $\alpha$, $R_F$, and $R_P$.

Each round constant is generated by obtaining challenge bytes from the Merlin transcript, derived using label round-constant. We obtain $(n+135)/8$ bytes where $n$ is the field size in bits. These bytes are then interpreted as an unsigned little-endian integer reduced modulo the field.

MDS Matrix

We generate MDS matrices using the Cauchy method. However instead of randomly sampling the field as described in the text, we deterministically generate vectors $x$ and $y$ as:

$x=[\mathrm{0..}t)$ $y=[t..2t)$

Each element $M_{ij}$ of the matrix is then constructed as:

$M_{ij}=\frac{1}{x_i+y_j}$

where $i,j\in [\mathrm{0..}t)$.

This deterministic matrix generation method has been verified to be safe over the base field of decaf377, using algorithms 1-3 described in Grassi, Rechberger and Schofnegger 2020 over the t range 1-100.

The parameters that are used for poseidon377 are located in the params.rs module of the source code. The parameters were generated on an Apple M1.